"Inni csak mértékkel és tartózkodással szabad. Mérték a vödör, tartózkodás az asztal alatt."
A fenti kép a hagyományos válasz erre a kérdésre. Azaz Legyen X tetszőleges halmaz, M az X részhalmazaiból álló σ-algebra és µ az M-n értelmezett nemnegatív σ-additív halmazfüggvény. Ekkor az (X, M, µ) hármast métréktérnek nevezzük, és az M halmaz elemeit mérhető halmazoknak nevezzük.
De ez alapján nekem számtalan sok kérdésem van. Mi az a σ-algebra? Hogy képzeljek el egy halmazsorozatot? Meg úgy egyáltalán mivaaan?
Kezdjük egy kicsit másképp:
A mérték egy függvény, ami egy adott halmaz részhalmaihoz egy számot rendel. Ez már kicsit szebben hangzik. Tehát a mértékelmélet arról szól, hogy halmazokhoz rendelünk számokat.
Ilyen például a távolság. Ahol a halmazunk elemei a pontok, a részhalmazok valahány pont kiválasztva, és a mérték 2 pont közti távolság, tehát egy szám.
Fenti tudásunkon felbátorodva, fussunk neki a formálisabb definíciónak!
Ω = alaphalmaz, melynek elemei az elemi események
A = az események σ-algebrája
Borel-mérhető halmaz = az összes értelmes halmaz, amit el lehet képzelni, tehát olyan halmazok, amik intervallumok rendszeréből a szokásos műveletekkel előállíthatók. Például egy Borel-halmaz a valós számok halmaza is.
Már csak a σ-algebrával és a σ-additivitással vagyok adós és máris érthető a mérték formális definíciója is.
σ-additívnak nevezünk egy halmazfüggvényt, ha értelmezési tartományába tartozó diszjunkt halmazok megszámlálható unióján is értelmezve van, és az itt felvett érték megegyezik az uniót alkotó halmazokon felvett értékeinek összegével.
Vegyük észre, hogy ez a területfogalom általánosítása. Fontos megjegyeznünk, hogy a meghatározásban nem hagyható el a diszjunkt szó. Mivel ha nem üres két halmaz metszete, akkor az uniójuk mértéke nem egyezik meg a mértékeik összegével. Lásd: szitaformula.Az unió elemszámára ugyanis a következő képlet teljesül:
A kivonást azért kell elvégezni, mert a metszet elemeire vonatkozóan az összeszámolásban |A| + |B| összegben kétszer végeztük el. Most képzeljünk az elemszámok helyére mindenhova mértéket. [ Lehet, hogy az elemszám is mérték? ;) ]
A σ-algebra Ω-n, ha- egyszerű halmaztestet képez (tehát algebra)
- Ω eleme A-nak- nem üres- zárt az elemei véges családjainak uniójára, metszetére, különbségére - elemei megszámlálhatóan végtelen sok tagú egyesítésre zárt
Most nyugodtan tekintsünk vissza az eredetileg bemásolt ijesztő képre. És lássuk be, hogy lehetne ennél rosszabb is a helyzet...
Ám ne aggódjatok a rosszabb rész majd holnap következik! Amikor ugyanis bevezetjük a valószínűségszámítás alapfogalmait MÉRTÉKelméleti alapon.


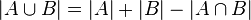
Nincsenek megjegyzések:
Megjegyzés küldése